经典算法题
第一部分:数组(Array)—— 核心:下标变换与双指针
数组面试题主要考查对边界的控制和对时间复杂度的压榨(通常要求 $O(n)$)。
1. 两数之和 (Two Sum)
-
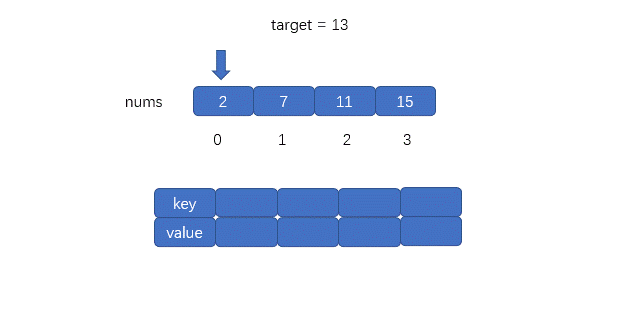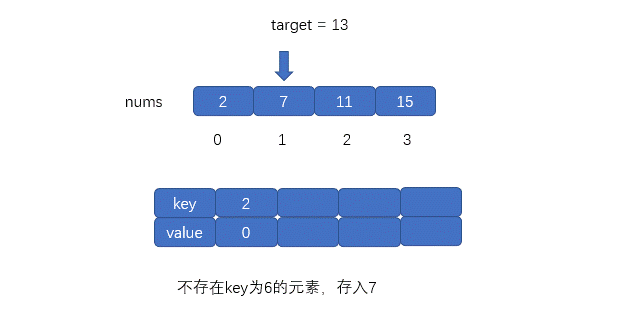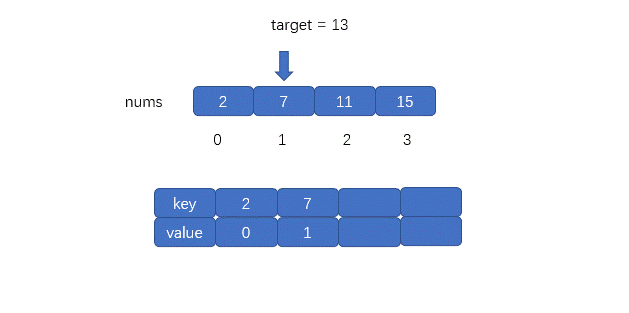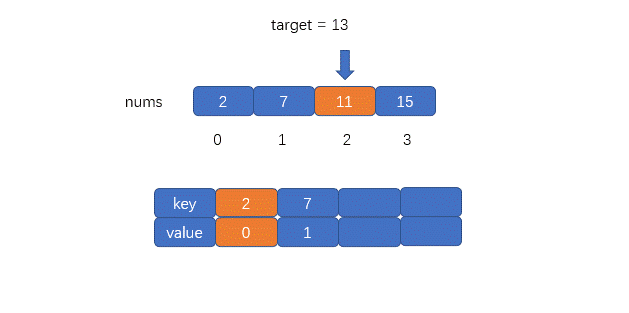
题目: 给定一个数组和一个目标值,寻找索引 $i, j$ 使得
nums[i] + nums[j] == target。 -
核心思维: 空间换时间。不要两层循环,遍历数组时用一个
Dictionary/HashMap存{ target - nums[i] : i }。 -
举一反三: 看到“寻找特定组合”,优先想哈希表。
class Solution {
List<int>? twoSum(List<int> nums, int target) {
final Map<int, int> resultMap = {};
for (int i = 0; i < nums.length; i++) {
int tempNum = target - nums[i];
if (resultMap.containsKey(tempNum)) {
return [resultMap[tempNum]!, i];
}
resultMap[nums[i]] = i;
}
return null;
// 如果没找到,返回 null
}
}
1.1 两数之和 有序数组 O(1)时间复杂度
题目:
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。
以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
你所设计的解决方案必须只使用常量级的额外空间。
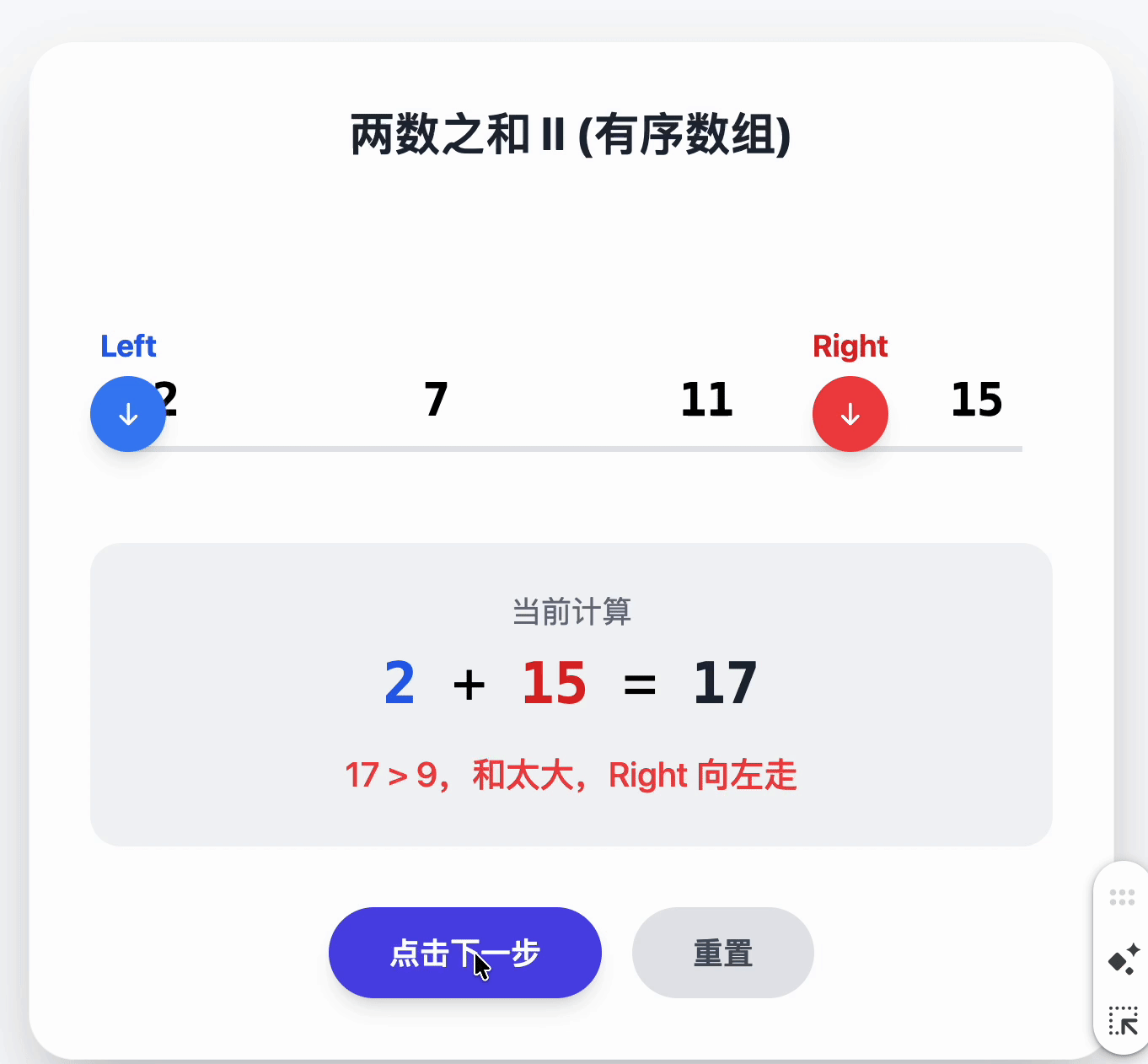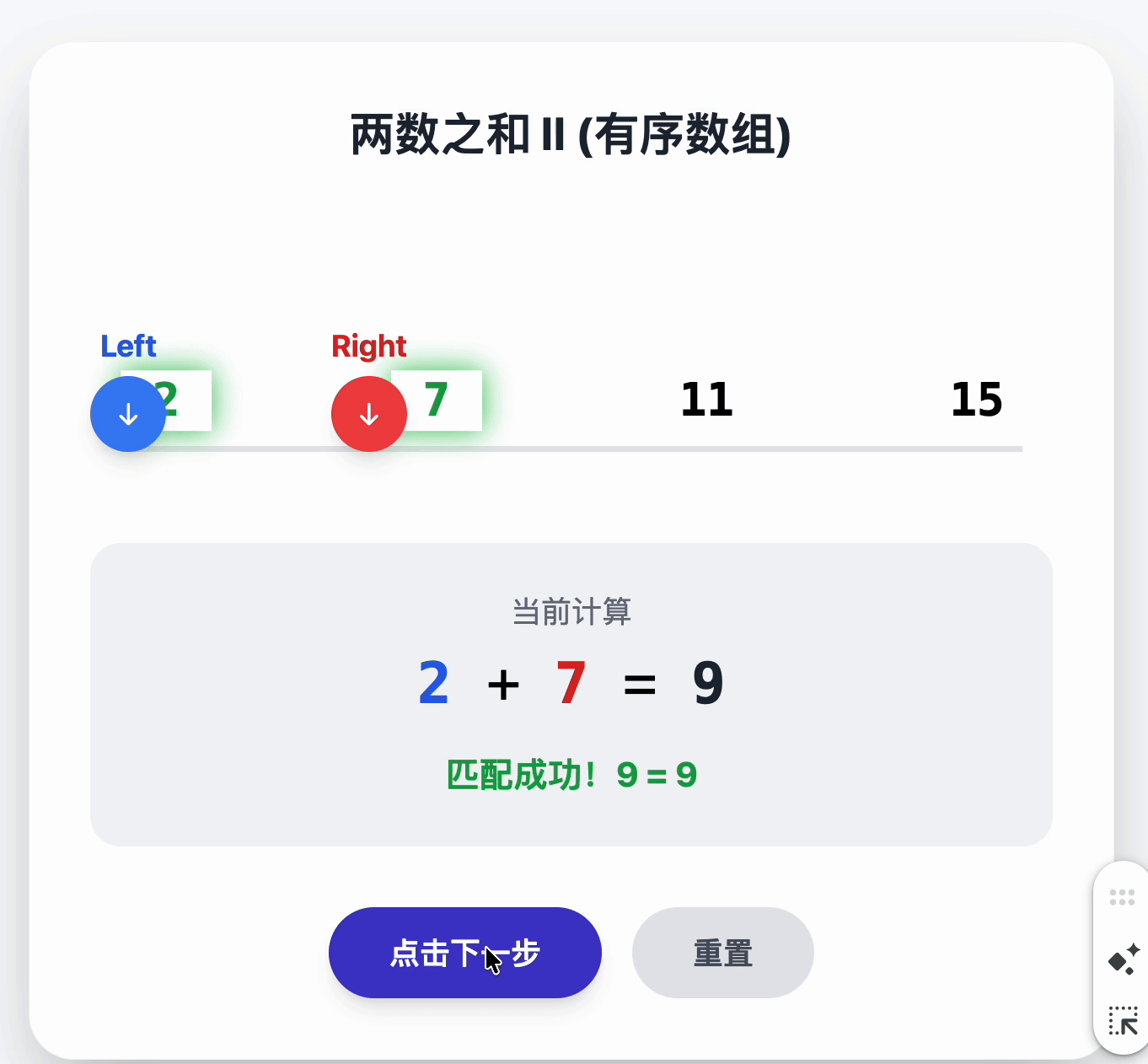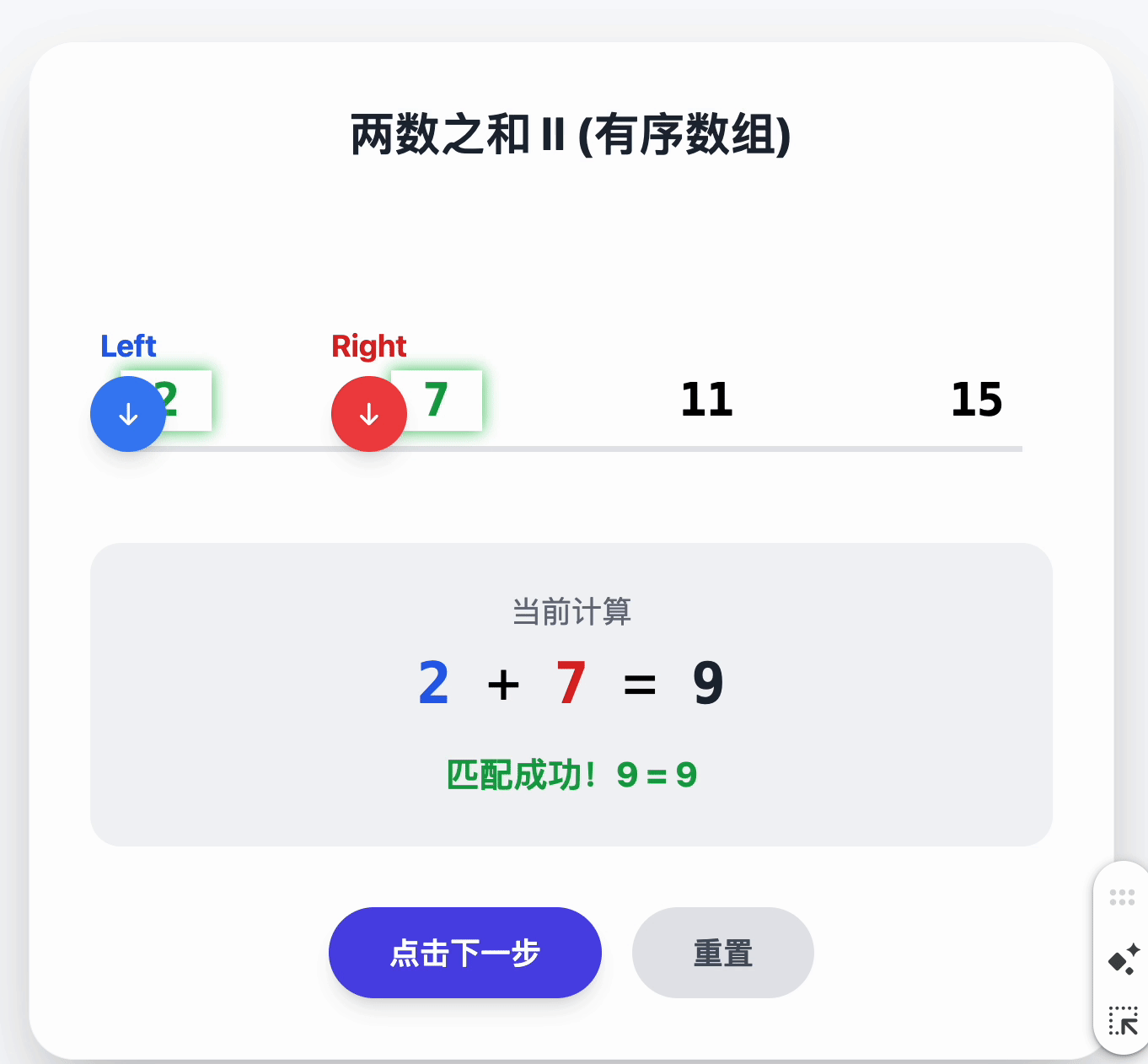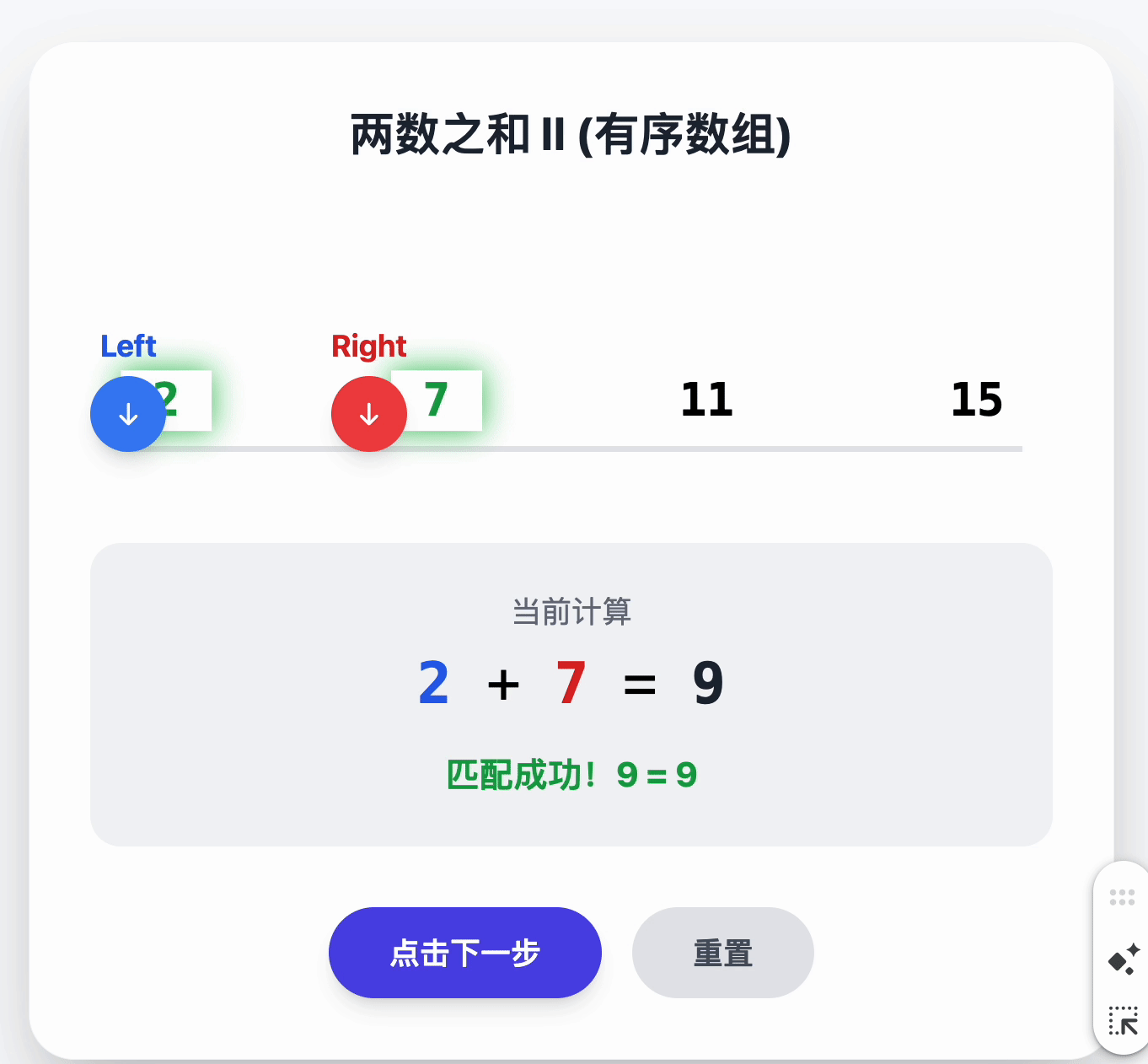
class Solution {
List<int>? twoSum(List<int> numbers, int target) {
int left = 0;
int right = numbers.length;
while (left < right) {
int sum = numbers[left]+ numbers[right-1];
if (target == sum) {
return [left+1,right];
}
if (target < sum) {
right--;
} else {
left++;
}
}
return null;
}
}
2. 三数之和 (3Sum)
-
题目: 找出所有和为 0 的不重复三元组。
-
核心思维: 排序 + 双指针。先排序,固定一个数
i,剩下的部分用左指针L和右指针R向中间夹。 -
举一反三: 在有序数组里找组合,双指针是不二法门。
3. 移动零 (Move Zeroes)
-
题目: 将所有 0 移到末尾,保持非零元素相对顺序。
-
核心思维: 快慢指针。慢指针
j指向“下一个非零数该放的位置”,快指针i遍历。 -
举一反三: “原地修改数组”、“去重”、“移动元素”类问题,都用快慢指针。
第二部分:字符串(String)—— 核心:滑动窗口
字符串本质是字符数组,但常涉及子串问题。
1. 无重复字符的最长子串
-
题目: 找到其中不含有重复字符的 最长子串 的长度。
-
核心思维: 滑动窗口 (Sliding Window)。用一个
Set或字典维护窗口内的字符,右边界往后移,遇到重复的,左边界被迫收缩。 -
举一反三: 只要题目出现“子串”(连续的),第一时间想滑动窗口。
2. 验证回文串 (Valid Palindrome)
-
题目: 忽略大小写和非字母数字字符,判断是否回文。
-
核心思维: 头尾双指针。注意过滤掉非字符(在 Swift 中用
isLetterNumber)。 -
举一反三: 判断对称性问题,用头尾指针。
3. 翻转字符串里的单词
-
题目:
"the sky is blue"->"blue is sky the"。 -
核心思维: 整体反转 + 局部反转。先把整个字符串反转,再逐个反转每个单词。
-
举一反三: 涉及到位置调整但不想申请额外大空间的,考虑多次反转。
第三部分:链表(Linked List)—— 核心:指针操作与哨兵节点
链表题不难,但极其容易在指针指向(死循环)和边界条件(头节点变化)上出错。
1. 反转链表 (Reverse Linked List)
-
题目: 将链表反转。
-
核心思维: 迭代三指针。维护
prev,curr,next三个指针,一边遍历一边改指向。 -
举一反三: 这是所有链表题的基础。
2. 环形链表 (Linked List Cycle)
-
题目: 判断链表中是否有环。
-
核心思维: 快慢指针 (Floyd 判圈算法)。快指针走两步,慢指针走一步,只要相遇就有环。
-
举一反三: 寻找链表的中点、寻找倒数第 K 个节点,都用这种“步长差”思维。
3. 合并两个有序链表
-
题目: 将两个升序链表合并为一个新的升序链表。
-
核心思维: 虚拟头节点 (Dummy Node)。先创建一个假的头节点,然后像拉链一样对比两个链表,谁小谁挂上去。
-
举一反三: 当你需要创建一个新链表,但又不确定头节点是谁时,必须用 Dummy Node,它能极大简化代码逻辑。